‘최고시속 150km’ 루지 선수가 느낄 인공중력 얼마나 될까?

최고 시속 150km로 달리는 겨울 스포츠, 루지. 출처: Wikimedia Commons

〔윤복원의 ‘물리상식으로 푸는 요즘 세상’〕
(1) 겨울올림픽과 구심력-원심력

최고 시속 150km로 달리는 겨울 스포츠, 루지. 출처: Wikimedia Commons

겨울 올림픽에는 속도감을 즐기는 경기 종목이 많다. 특히나 경기장에 곡선 구간이 있어 역동성을 더하는 쇼트트랙과 루지 경기에서는 구심력과 원심력이 승부에서 중요하게 작용하기에 선수들이 이에 잘 적응하는 것도 좋은 성적을 거두는 데 관건이 된다. 선수들은 곡선 구간에서 얼마나 큰 구심력 또는 원심력을 경험할까?

시애틀 기차 탈선사고의 곡선 구간

지난 12월18일 미국 시애틀에서, 달리던 기차가 철길에서 벗어나는 대형 탈선 사고가 일어났다. 뉴스를 보면 “제한 속도가 시속 30마일(시속 48.3km)인 구간을 시속 78마일(시속 125km)로 달리다가 탈선했다”고 한다.[1] 일반적으로 기차는 평균 시속 100km 이상의 고속으로 달린다는 점을 감안하면, 사고가 날 때 기차의 속도는 지나치게 높지는 않았던 것처럼 보인다. 하지만 사고가 난 곳은 기차의 최고 속도를 시속 50km보다 낮게 제한하는 곳이었다. 구글 지도(아래)를 통해, 이곳 철길이 어떤 구조였는지 보면 제한 속도가 왜 이렇게 낮은지를 알 수 있다..

반듯하게 일직선으로 만들어진 고속도로에서는 제한 속도가 대체로 시속 100km 이상이다. 도로 상태와 날씨가 좋으면 시속 100km로 달려도 웬만해서는 큰 문제가 없다. 물론 앞차와 충분한 거리를 유지해야 한다. 그런데 산을 넘어가는 꼬불꼬불한 길에서는 고속도로에서 달리듯이 빠르게 달릴 수 없다. 그랬다간 차가 미끌어지면서 휘어진 도로의 바깥 방향으로 밀려날 수 있다. 심하면 차가 옆으로 굴러 뒤집힐 수도 있다. 이 때문에 꼬불꼬불한 도로에서는 제한 속도가 훨씬 낮게 정해진다.

구글 지도로 확인할 수 있는 시애틀 탈선 사고 지점의 철길도 직선이 아닌 곡선 구간이다. 바로 이 점이 제한 속도가 평균 속도보다 낮은 이유와 관련돼 있다. 더 많이 휜 곳일수록 더 천천히 달려야 하는 것을 감안하면, 제한 속도가 시속 50km에 못 미치는 사고 지점에서는 철길이 상당히 많이 휘어 있음을 짐작해 볼 수 있다. 그러면 탈선 사고가 난 곳은 철길이 얼마만큼 휘어져 있었을까?

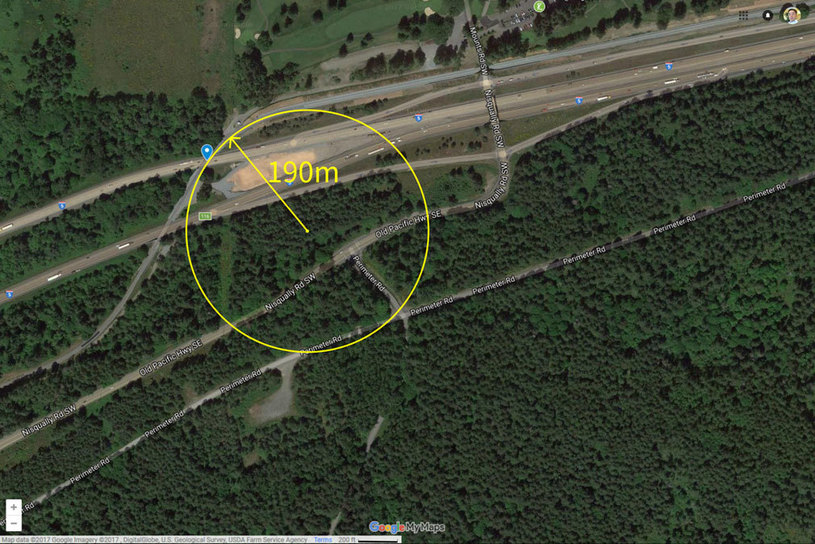
휘어진 정도를 표현하는 값의 하나로 “곡률 반지름”(radius of curvature)이 있다. 휘어진 부분에 가장 잘 들어맞는 동그라미의 반지름이다. 시애틀의 탈선 사고가 일어난 곳을 구글 지도에서 찾아 확인해보면, 아래 그림과 같이 가장 많이 굽은 곳이 반지름이 190m인 동그라미와 잘 들어맞는다. 곡률 반지름이 대략 190m임을 알 수 있다. 기차가 이 구간을 지나갈 때 부분적으로 반지름이 190m인 동그라미 모양으로 움직이는 ‘원운동’을 한다고 볼 수 있다는 얘기다.

2017년 12월 18일 미국 워싱턴주 시애틀에서 발생한 기차 탈선 사고 지점의 위성사진(구글 맵). 가장 많이 휜 철길의 곡률 반지름은 대략 190m이다.

뉴튼의 제1 운동법칙인 ‘관성의 법칙’에 의하면, 아무런 힘이 없는 상황에서는 직선으로 움직이는 것이 자연스러운 움직임이다. 휘어진 궤적을 따라 움직인다는 것은 직선을 따르지 않고서 방향을 바꾸며 움직인다는 것을 의미한다. 그럴려면 움직이는 물체의 방향을 바꿔주는 힘이 있어야 한다. 동그라미 모양으로 움직이는 ‘원운동’에서는 이런 힘을 구심력이라고 부른다. 일정한 속력으로 원운동을 하는 경우에 구심력의 방향은 원의 중심을 향한다.

자동차가 휜 도로를 달릴 때, 자동차는 부분적으로 원운동을 한다. 구심력이 필요한 경우다. 도로 바닥이 자동차 바퀴를 안쪽으로 미는 힘, 다시 말해 도로 바닥과 자동차 바퀴가 맞닿은 경계면 사이의 마찰력이 구심력의 역할을 한다. 기차의 경우는 철길이 기차를 미는 힘이 구심력이다.

뉴튼의 제3 운동법칙인 ‘작용-반작용의 법칙’은, ‘A라는 물체가 B라는 물체에 힘을 준다면(작용), B물체도 A물체에 크기는 같지만 방향이 반대인 힘을 준다(반작용)’는 법칙이다. 기차가 원운동을 하는 동안 철길이 기차를 안쪽으로 밀 때, 기차는 같은 크기의 힘으로 반대 방향인 바깥쪽으로 철길을 민다. 철길이 기차를 미는 힘이 구심력이고, 이에 대한 ‘반작용’인 기차가 철길을 미는 힘을 종종 원심력으로 보기도 한다. 하지만 엄밀하게 따지면 기차가 철길을 미는 힘, 다시 말해 철길이 받는 힘이어서, 우리가 일상에서 느끼는 원심력과는 다르다고 보는 것이 적절하다.

한편 원운동 하는 기차는 안에 타고 있는 승객을 다시 안쪽으로 민다. 관성의 법칙으로 승객도 아무런 힘이 없으면 직선으로 움직여야 하는데 그렇지 않고 기차와 같이 원운동을 한다. 승객이 원운동을 하게 하는 힘은 기차가 승객을 안쪽으로 미는 힘이다. 앉아 있는 승객은 의자가 엉덩이 부분을, 서 있는 승객은 바닥이 발바닥을 원운동 안쪽 방향으로 민다. 이때 몸의 다른 부분이 상대적으로 원운동 바깥 방향으로 밀리면서, 승객은 마치 바깥 방향을 향하는 힘이 몸을 민다고 느낀다. 원운동을 할 때 이렇게 바깥으로 밀린다고 느끼는 힘이 바로 우리가 일상적으로 느끼는 원심력이다.

하지만 이 원심력은 실제 존재하는 힘이 아니다. 직선으로 움직이려는 관성과 몸의 일부분을 기차가 안쪽으로 당기는 것이 복합적으로 작용해, 마치 바깥 방향으로 작용하는 힘이 있다고 느낄 뿐이다. 이러한 원심력을 중력과 구분하기 어려워 ‘인공중력’으로 보기도 한다. 우리가 중력이라고 느끼는 힘도 사실은 중력에 대항해 우리를 떠받치는 힘이듯이, 인공중력이라고 느끼는 힘은 구심력이 미는 힘을 느끼는 것이다.

구심력과 원심력 어떻게 계산할까

물체가 원운동을 하는 데 필요한 구심력의 크기를 어떻게 계산할까? 일정한 속도로 원운동을 하는 경우, 물체가 움직이는 모양인 원의 반지름과 물체의 속도, 그리고 물체의 질량을 알고, 이 값들을 아래의 수식에 넣어서 구심력을 계산하면 된다. 원의 바깥 방향으로 작용한다고 느끼는 힘인 ‘원심력’의 크기도 구심력의 크기와 같다. 방향만 반대일 뿐이다.

구심력 또는 원심력 크기 = (질량 x 속도 x 속도) / 반지름 = (질량 x 속도²) / 반지름

수식을 보면, 질량이 클수록 구심력 또는 원심력도 커진다. 만약에 지표면의 중력 크기(= 질량 x 중력가속도)를 기준으로 구심력이나 원심력의 상대적인 크기로 나타내면, 질량에 관계없이 “지표면 중력의 몇 배다”라는 식으로 표현할 수 있다.

자동차 또는 기차의 속도는 보통 시속 몇 km인지로 표시한다. 곡률 반지름을 m로 표시하는 경우라면 지표면 중력 크기 대비 구심력 또는 원심력의 크기는 아래와 같이 변형된 수식으로 계산하면 된다.

구심력 또는 원심력 크기(지표면 중력 크기 대비) = 속도(km/h)² / (127 × 곡률반지름(m))

곡률 반지름이 190m인 철길을 제한 속도인 시속 48.3km로 달리면 구심력 또는 원심력의 크기는 지표면 중력의 0.097(=9.7%) 배이고, 시애틀 탈선 사고 당시 기차가 달렸던 시속 125km로 달리면 지표면 중력의 0.65(=65%) 배라는 계산 결과가 나온다. 제한 속도로 천천히 사고 지점을 달리면 기차 안에 있는 승객은 약한 크기의 인공중력을 느끼는 반면, 사고 당시 속력인 시속 125km로 사고 지점을 달리면 승객은 기차가 도는 바깥 방향으로 중력의 65%에 이르는 인공중력을 느낀다.

기차가 곡선 구간을 지나갈 때 필요한 구심력은 철길이 기차의 바퀴를 곡선 구간 안쪽으로 미는 힘이다. 사고 당시 지나치게 빨리 달리는 기차가 곡선 구간에서 탈선하는 것은 철길이 기차 바퀴를 미는 힘이 필요한 구심력에 비해 충분하지 못해서 일어났을 가능성이 있다. 한편 철길이 기차의 바퀴를 안쪽으로 미는 구심력이 충분해도, 기차의 윗부분은 철길이 안쪽으로 밀어주는 힘을 직접 받지 않아 바깥으로 밀린다. 마치 회전하는 버스 안에 서 있는 사람의 몸 윗부분이 바깥 방향으로 밀리는 것과 비슷하다. 버스 안에 서 있는 사람과 마찬가지로, 사고 기차도 회전하는 바깥 방향으로 기차 윗부분이 밀려서 기울다가 넘어졌을 가능성도 있다.

쇼트트랙 경기의 구심력과 원심력

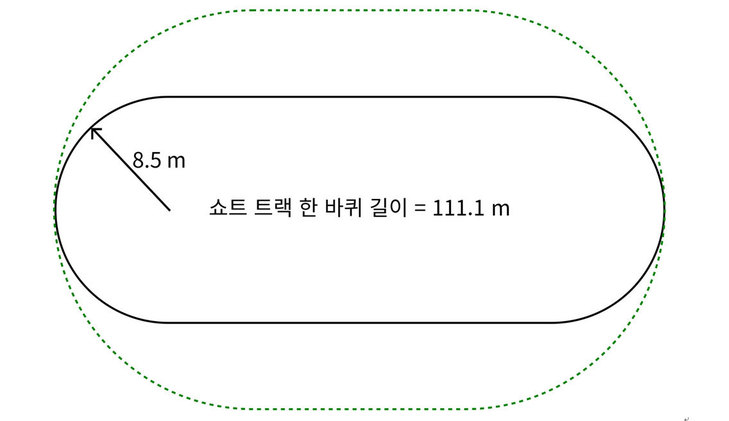
겨울 올림픽 경기종목의 하나인 쇼트트랙은 구심력과 원심력이 중요한 경기다. 먼저 쇼트트랙 경기장이 어떤 규격으로 만들어졌는지를 보자. 쇼트트랙 한 바퀴 길이는 111.1m이다. 그중 양쪽 곡선 구간은 선수들이 스케이크를 타는 경로를 기준으로 반지름이 8.5m인 원을 반으로 자른 모양이다. 곡률 반지름이 8.5m인 곡선 구간이다. 최단 거리로 스케이트를 탄다면 곡선 구간에서는 반지름이 8.5m인 원 모양으로 움직이는 원운동을 하는 셈이다..

쇼트트랙 500m와 1000m 경기에서 세계 정상급 선수들의 기록은 40초와 1분 20초(100초) 근처다. 쇼트트랙의 정확한 경로로 스케이트를 탄다면 평균 속력은 초속 12.5m 정도라고 볼 수 있다. 하지만 실제 경기에서는 트랙의 경로를 정확히 따라가지 않고 좀 더 완만하고 큰 곡선으로 선수들이 스케이트를 탄다. 그 만큼 더 긴 거리를 달리게 되어, 평균 속력은 초속 12.5m보다는 크다고 볼 수 있다. 여기에 더해 쇼트트랙 경기 특성상 결승선에 가까워졌을 때 더 빨리 달리기 때문에, 경기 후반부만 따로 계산하면 평균 속력이 더 크다. 반면 곡선 구간에서는 선수들이 가속을 하지 않고 달린다. 이 때문에, 구선 구간의 속력은 직선 구간의 속력보다는 더 작다. 이런 점들을 고려하면 올림픽 결승과 같은 경기에서 최상급 선수가 전력질주 하는 경우, 경기 막판에 곡선 구간에서의 속력을 초속 12.5m로 잡는 것은 무리 없어 보인다.

쇼트트랙 크기: 트랙 한 바퀴 길이는 111.1m이다. 트랙의 직선 구간 길이는 총 28.8m×2 = 57.7m이고 트랙 양쪽에 있는 곡선 구간 각각은 선수들의 스케이팅 경로를 기준으로 반지름이 8.5m(곡률 반지름이 8.5m)인 원의 반쪽 모양으로, 총 2π8.5=53.4m이다. 실제 경기에서 선수들은 초록색 점선 경로와 같은 좀 더 완만하게 도는 경로로 스케이트를 탄다. 그 만큼 곡률 반지름이 커져서 같은 속도로 달린다면 곡선 경로에서의 구심력과 원심력이 더 작아지고, 같은 구심력(또는 원심력)을 유지하면 더 큰 속도를 낼 수 있다.

폭이 30m가량인 쇼트트랙 링크 전체를 활용하면 곡선 구간의 곡률 반지름이 최대 15m까지 늘어난다. 그럴려면 경기장 가장자리를 돌아야 하는데, 실제 경기에서는 그 정도까지 경기장을 크게 돌지는 않는다. 따라서 실제 경기에서 선수들이 도는 곡선 구간의 곡률 반지름은 8.5m과 최대 15m 사이가 된다. 이를 근거로 선수들이 스케이트를 타는 실제 곡선 구간의 곡률 반지름을 중간값 근처인 대략 12m라고 가정해 보자.

초속 몇 m로 달리는지로 속력을 나타내고, 곡률 반지름을 m로 나타내면, (지표면 중력 크기 대비) 구심력 또는 원심력 크기는 아래의 수식으로 계산할 수 있다.

구심력 또는 원심력 크기 (지표면 중력 크기 대비) = 속도(m/h)² / (9.8 × 곡률 반지름(m))

초속 12.5m의 속력과 곡률 반지름 12m로 최상급 선수가 마지막 곡선 구간을 달릴 때 필요한 구심력 또는 원심력의 크기를 계산하면, 그 값은 지표면 중력의 1.33배가 된다. 이때 구심력은 얼음이 스케이트 날을 곡선 구간 안쪽으로 미는 힘이다. 한편 선수는 구심력과 크기와 같지만 방향이 다른 원심력을 느낀다.

방향은 수평 방향으로 곡선 구간 바깥쪽을 향하면서 크기는 중력의 1.33배인 인공중력이 추가로 생기는 것이다.

곡선 구간에서 스케이트를 타는 실제 선수들의 모습: 몸이 기울어진 각도는 45도보다 더 뉘어진 각도다. 45도로 기울어져 달릴 때 원심력과 중력은 같은 같은 크기다. 반면, 45도보다 바닥으로 더 기울면 원심력이 중력보다 더 큰 경우고, 45도보다 덜 기울면 중력이 원심력보다 큰 경우다. 사진 출처: Wikimedia commons

쇼트트랙 곡선을 돌 때 몸을 얼마나 기울여야 하나

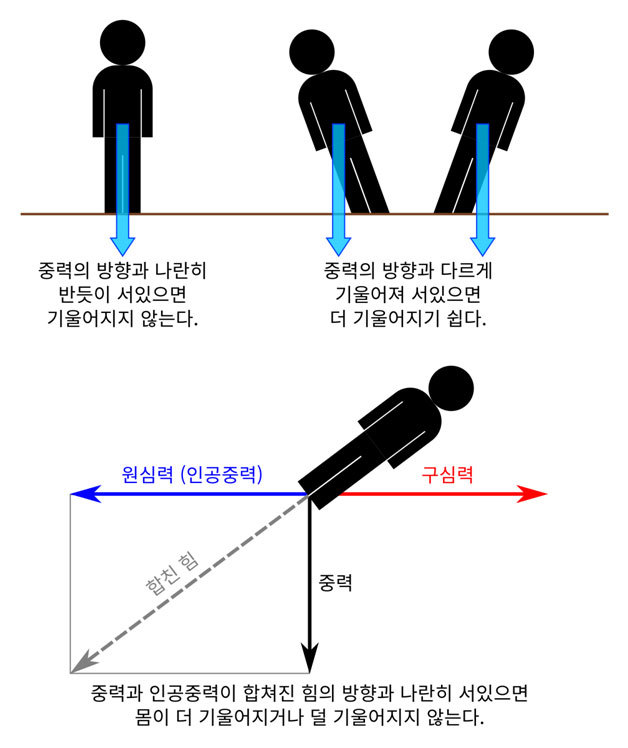
우리가 서 있을 때 중력의 방향과 같은 방향인 수직으로 서 있으면 웬만해서 넘어지지 않는다. 마찬가지로 쇼트트랙의 곡선 구간에서는, 원심력으로 인한 인공중력과 실제 중력이 합쳐진 힘이 향하는 방향에 맞추어 몸이 나란히 있어야 넘어지지 않는다.

그러면 ‘합쳐진 힘의 방향’은 어떻게 알 수 있을까? 중력과 인공중력의 크기를 고려해 직사각형을 그리면 합져진 힘을 방향을 알 수 있다. 수직인 변의 길이는 중력의 크기이고 수평인 변의 길이는 인공중력의 크기인 직사각형을 그렸을때, 직사각형에서 대각선 방향이 합쳐진 힘의 방향이다. 그리고 대각선의 길이가 그 크기가 된다.

원심력이 중력의 1.33배인 경우에는 수직인 변의 길이가 1이고 수평인 변의 길이는 1.33인 직사각형을 그리면 된다. 이 직사각형의 대각선 방향이 중력과 인공중력이 합쳐진 힘의 방향으로, 수직 방향보다 53도 더 기운 방향이다.[2] 선수 몸이 이 방향과 나란히 있으면 몸이 더 기울거나 덜 기울지 않게 된다. 실제 경기 장면을 보면 곡선 구간에서 선수들의 몸이 상당히 기울어진 채로 달리는 것을 볼 수 있다. 대각선의 길이는 1.66이다. 지표면 중력의 1.66배의 중력을 느낀다는 의미다.

중력의 방향 또는 중력과 인공중력이 합친 힘의 방향과 몸이 나란히 있을때 몸이 더 기울지 않는다. 아래그림에서 직사각형에서 수직 방향의 변의 길이가 중력의 크기와 같고 수평방향의 변의 길이가 원심력의 크기와 같으면, 대각선의 길이는 중력과 원심력이 합쳐진 힘의 크기가 된다. 합친 힘을 방향은 대각선 방향이다.

중력과 인공중력이 합쳐진 힘의 방향이 기울어져 있으므로, 곡선 구간에서 스케이트를 타는 선수가 느끼는 중력의 방향도 기울어져 있다. 이 때문에 수평인 경기장 얼음바닥은 곡선 구간을 도는 선수에게는 기울어진 바닥이나 마찬가지다. 가만히 서 있는 사람은 기울어진 얼음바닥에서 더 잘 미끌어지는 것처럼, 곡선 구간을 도는 선수를 중심으로 보면 중력과 원심력이 합쳐진 힘의 방향과 직각이 아닌 경기장 얼음바닥에서는 더 쉽게 미끌어진다. 실제 경기중에 선수들이 미끌어지는 곳은 주로 곡선 구간이다.

곡선 구간을 달릴 때 바닥에서 덜 미끄러지려면, 중력과 인공중력이 합쳐진 힘의 방향과 직각이 되게 경기장 바닥이 기울어져 있으면 된다. 가만히 서 있는 사람을 기준으로 따지면 수평인 얼음 바닥에 서 있는 것과 유사한 상황이 만들어지기 때문이다. 그러나 쇼트트랙 곡선 구간은 직선 구간과 마찬가지로 수평으로 만들어져 있어, 곡선 구간에서 빠른 속력을 내는 것이 쉽지 않다.

‘횡경사’ 있는 벨로드롬과 루지 경기장

곡선 구간에서 미끌어지지 않도록 아예 바닥 구조를 달리 만든 경기장이 있다. 자전거 경주를 하는 벨로드롬(velodrome)이 그런 경우다. 벨로드롬 트랙은 안쪽은 낮고 바깥쪽은 높게 만들어져 있다. 자전거를 타고 달리는 선수입장에서는 좌우로 기울어진 구조로, ‘옆으로 경사져 있다’는 의미로 횡경사(banking)라고도 부른다. 올림픽 경기때 사용하는 벨로드롬의 경우 곡선 구간의 횡경사 각도는 최대 45도에 이른다.

앞에서 설명했듯이, 바닥이 중력의 방향과 직각으로 만들어져 있으면,[3] 그 바닥 위에 서 있는 사람도 바닥과 몸이 직각을 이루어 쉽게 미끌어지지 않는다.[4] 벨로드롬의 곡선 구간을 달리는 선수는 중력과 원심력이 합쳐진 힘의 방향으로 자전거와 몸을 기울이면서 달린다. 그래야 자전거와 몸이 더 기울거나 덜 기울지 않기 때문이다. 이때 횡경사 구조로 만든 바닥은 몸과 직각에 가깝게 되고, 선수가 느끼는 중력과 인공중력이 합쳐진 힘과도 직각에 가깝게 된다.[5] 마치 수평의 바닥에 서 있는 것과 같은 상황이어서 쉽게 미끌어지지 않는다.

벨로드롬 내부 전경을 보여주는 사진: 전 구간에서 경기장 바닥이 경사져 있음을 볼 수 있다. 특히 곡선구간에서의 횡경사 각도가 큼을 알 수 있다. 출처: Wikimedia Commons

그런데 문제는 원심력(또는 구심력)의 크기가 자전거의 속도에 따라 변한다는 점이다. 하지만 선수들이 달리는 평균 속력에 맞쳐 경기장 바닥을 만들면 일부 편차는 있겠지만, 자전거와 선수는 횡경사의 경기장 바닥과 약간의 오차로 직각과 가깝게 되어 쉽게 미끌어지지 않는다. 약간 기울어진 바닥에 서 있어도 바닥의 마찰력 때문에 미끌어지지 않는 것과 마찬가지다.

탈선사고가 일어난 시애틀 철길의 곡선 구간도 벨로드롬의 곡선 구간만큼은 아니더라도 충분한 횡경사의 구조로 만들어졌으면 어땠을까 하는 생각도 해봄직하다. 중력과 원심력이 힘쳐진 힘의 방향이 철길 바닥과 좀 더 직각에 가까워져서, 기차가 기울어져서 생기는 탈선 가능성은 줄어들 수 있기 때문이다.

매우 빠른 속도로 썰매를 타는 루지(luge)라는 경기가 있다. 동계 올림픽 경기 종목 중에 속도가 가장 빠른 경기라고 한다. 최고 속력은 시속 150km에 이르고,[6] 곡선 구간에서는 원심력으로 인한 인공중력이 지구 중력에 비해 최대 5배에 이른다고 한다. 쇼트트랙 스케이팅과 달리 이런 엄청난 속도임에도 선수들이 트랙에서 벗어나지 않는 이유는 자전거 경주의 벨로드롬처럼 일종의 횡경사가 만들어져 있기 때문이다.

루지 경기장의 곡선 구간에서 썰매를 타고 있는 선수의 모습. 횡경사(banking)가 수직에 가까워 마치 얼음벽을 타고 가는 모양새다. 원심력으로 인한 인공중력이 지표면 지구 중력보다 훨씬 큰 경우에 이런 상황이 만들어진다. 이때 선수의 썰매가 지나가는 얼음 바닥은 원심력과 지구중력이 합쳐진 힘과 거의 직각이다. 출처: Wikimedia Commons

원심력이 지구중력의 5배이면 사실상 수직에 가깝게 횡경사가 만들어져야 하는데, 실제 루지 경기장의 곡선 구간에서는 얼음바닥이 90도(수직)보다 적은 각도에서 90도보다 큰 각도를 아우르게 반 원통형과 가까운 모양으로 얼음 트랙이 만들어져 있다. 곡선 구간에서 천천히 달리면 약간만 기울어져서 달릴 수 있고, 빠르게 달리면 수직에 가깝게 기울어져 달릴 수 있는 구조다.

하지만 2010년에 뱅쿠버 올림픽을 앞둔 훈련 경기 중에 곡선 구간을 지나자마자 선수가 썰매에서 튕겨져 나와 기둥에 부딪히면서 사망하는 사고가 있기도 했다. 선수가 튕겨 나가기 직전에 마지막 곡선 코스를 달릴 때의 속도는 초속 39.81m로 시속 143km에 육박했다.[7] 이 속도와 곡선 코스의 곡률 반지름 33m로 계산한 구심력 또는 원심력의 크기는 지표면 중력 대비 4.9배에 이른다. 사고 직전 곡선 구간에서 선수는 지구 중력의 4.9배인 인공중력을 추가로 경험했다는 얘기다.

내친김에 원심력과 구심력의 이야기를 우리 주변의 가전제품과 친근한 영화를 통해 더 살펴보자.

세탁기의 원심력 이용 어떻게?

사람이 손으로 직접 빨래의 물기를 제거할 때에는 빨랫감 양쪽을 다른 방향으로 돌려서 꽈배기 모양처럼 쥐어짜서 물기를 제거한다. 세탁기는 쥐어짜는 방법 대신 세탁통을 돌리는 방법을 사용한다. 요즘 세탁기는 탈수할 때 세탁통이 1분에 1000번 이상 회전한다. 세탁통은 함께 도는 빨래를 구심력으로 밀고, 같이 도는 빨래에는 원심력으로 인한 강한 인공중력이 만들어진다. 인공중력의 방향은 세탁통 바깥으로 향한다. 빨래는 세탁통 벽에 걸려 있고, 젖은 빨래 속에 있는 물은 인공중력 방향인 세탁통 바깥 방향으로 흘려 내려가 세탁통에 있는 구멍으로 빠져 나간다. 젖은 빨래를 빨래줄에 걸어 놓으면, 물이 중력 때문에 아래로 흘러내리는 것과 마찬가지다. 세탁기 속에 만들어지는 인공중력이 훨씬 크기 때문에 그만큼 빨래 속에 있는 물이 더 잘 흘러나온다고 보면 되겠다.

1분에 세탁통이 돌아가는 회전수(rpm)와 세탁통의 반지름(m)을 알면, 아래 수식을 사용해 지표면 중력 대비 세탁통 바로 안쪽의 인공중력 크기를 계산할 수 있다.

지표면 중력 대비 세탁통의 인공중력 = (반지름(m) × (1분당 회전수)²) / 894

세탁통의 반지름이 0.25m(=25cm)이고 회전수가 1000rpm이면, 세탁통 바로 안쪽의 인공중력 크기는 지표면 중력의 280배에 이른다.

우주선에서 인공중력 만들기 어떻게?

맷 데이먼 주연의 영화 <마션(Martian)>에는 지구와 화성을 오고가는 헤르메스(Hermes)라는 우주선이 나온다. 이온 추진기로 가속하면서 행성 사이를 이동하는 헤르메스 우주선은 아주 천천히 가속하기 때문에 특별한 장치가 없으면 우주선 안에서는 거의 무중력 상태가 된다. 수백일 동안 우주에서 생활하는 우주인들은 인공으로 중력을 만든 공간에서 생활한다.

헤르메스 우주선에서 인공으로 중력을 만드는 방법은 세탁기에서 세탁통이 회전해 원심력으로 인공중력을 만드는 방식과 다를 바 없다. 반지름이 약 15m 정도로 크고[8] 훨씬 천천히 돌 뿐이다. 지구 표면의 중력과 같은 인공중력을 만든다고 하자. 이때 반지름을 알고 있으면, 헤르메스의 우주인 거주 공간이 얼마나 빠르게 돌아야 하는지는 아래의 수식을 사용해 계산할 수 있다.

한 바퀴 도는 데 걸리는 시간 = 6.283 × √(반지름(m) / 9.8)

반지름이 15m이면 7.77초에 한 바퀴를 돌아야 지구 표면의 중력과 같은 크기의 인공중력이 만들어진다. 이때 우주인 거주 공간은 길이가 94.2m(2π × r = 2 × 3.14 × 15)인 원둘레를 7.77초에 돌아서, 초속 12.1m의 속력으로 원운동을 하게 된다.

영화 <마션>에 나오는 우주선 ’헤르메스’. 회전력을 이용해 인공으로 중력을 만든다. 출처: 영화 <마션>

여기에서 재미있는 상황을 생각해볼 수 있다. 먼저 헤르메스 우주선의 거주 공간이 도넛 모양으로 다 뚫려 있고, 위에서 설명한 대로 7.77초에 한 바퀴씩 돌아 초속 12.1m의 속력으로 돈다고 가정하자. 그리고 우주인은 거주 공간이 돌아가는 방향과 반대로 뛰고, 뛰는 속력은 100m를 20초에 뛰는 초속 5m라고 하자.

우주인은 거주 공간이 돌아가는 방향과 반대 방향으로 뛰는 만큼, 우주인은 거주 공간보다 더 천천히 돈다. 우주선 밖에서 볼때 우주인의 원운동을 하는 속력은 거주 공간 속력인 초속 12.1m보다 초속 5m이 적은 초속 7.1m가 된다. 반지름이 15m이고 속력이 초속 7.1m인 원운동에서 원심력(또는 구심력)은 지표면 중력 대비 7.1² ÷ (9.8 × 15) = 0.34 배가 된다. 이 우주인은 지표면 중력의 1/3밖에 안되는 인공중력을 경험하게 된다.

우주인이 이번에는 초속 5m의 속력으로 거주공간이 도는 방향으로 달린다고 하자. 그러면 우주인은 거주 공간이 도는 속력인 초속 12.1m에 달리는 속력인 초속 5m가 더해져 초속 17.1m로 거주 공간보다 더 빨리 원운동을 한다. 17.1² ÷ (9.8 × 15) = 1.99 배가 된다.[9] 이 우주인이 느끼는 인공중력의 크기는 지표면 중력의 2배 가까이 된다. 달리는 방향에 따라 우주인이 느끼는 인공중력의 크기가 변한다는 얘기다.

같은 배우가 주연으로 나오는 또 다른 영화 <엘리시움’(Elysium)>에서는 지름이 60km에 이르는 거대한 우주정거장이 나온다. 이곳도 회전을 해서 원심력으로 인공중력을 만든다. 이 경우 지구 표면의 중력과 같은 크기의 인공중력을 만들기 위해서는, 우주정거장이 348초(= 6분 48초)에 한 바퀴를 돌아야 한다. 거주 공간이 도는 속력은 초속 542m가 된다. 이 정도 속력에서 사람이 뛰거나 자동차로 달려도 속력의 변화는 크지 않기 때문에 인공중력의 크기도 별로 변하지 않는다. <마션>의 헤르메스 우주선에 비해, 지구 표면의 중력 환경과 훨씬 더 유사한 인공중력 환경이 만들어진다고 볼 수 있겠다.

[주]

[1] The Amtrak Derailment Was Caused by a Collective Failure, 2017년 12월 24일, <뉴욕타임즈>, https://www.nytimes.com/2017/12/24/opinion/amtrak-derailment-seattle.html

[2] 곡선 구간에서는 선수들이 기울어져 달리기 때문에, 달리는 선수들의 몸 윗부분이 그리는 궤적은 스케이트 날이 그리는 궤적보다 더 안쪽에 있다. 따라서 몸 윗부분 궤적의 곡률반지름은 스케이트 날 궤적의 곡률반지름보다 작게된다. 동심원에서 안쪽에 있는 원의 반지름이 더 작은 것을 생각하면 되겠다. 이 때문에 몸 윗부분에 작용하는 원심력의 크기는 상대적으로 작고, 그만큼 기울어진 정도도 작아야 한다.

[3] 좀 더 엄밀하게 말하면, 중력에 대항해 바닥이 미는 힘과 바닥이 직각이 된다는 표현이 더 적절하다.

[4] 바닥과 발바닥 사이에 최소한의 마찰력을 필요하다.

[5] 이 부분도 좀 더 엄밀하게 말하면, 중력에 대항해 바닥이 미는 힘과 원운동에 필요한 구심력의 합쳐진 힘이 바닥에 직각이 된다는 표현이 더 적절하다.

[6] “Coroner‘s report into the death of Kumaritashvili, Nodar.”, T. Pawlowski, British Columbia Ministry of Public Safety and Solicitor General, 2010. Case No: 2010-0269-0002.

[7] Luge Track Safety, Mon hubbard, arXiv: 1212.4901v1 (2012)

[8] 영화에서 우주선 거주 공간이 돌아가는 장면에서 추정한 반지름이다.

[9] 지표면 중력의 2배 가까이되는 인공중력 상황에서는 초속 5m로 달리는 것도 어려울 수 있다. 이런 경우에는 롤러 스케이트를 탄다던가 전동 킥보드를 타고 달리는 경우도 생각해 볼 수 있겠다.

윤복원 미국 조지아공대 연구원(전산재료과학센터·물리학) [e-mail]