맛있는 것만 먹고 좋은 곳만 다니는 ‘잘나가는 페친’들의 비결은?

김범준 성균관대 물리학과 교수.

김범준의 인간관계의 물리학
①친구 관계의 역설

김범준 성균관대 물리학과 교수.

김범준 성균관대 물리학과 교수는 사회를 과학적인 방법으로 바라보는 연구에 관심이 많은 통계물리학자다. 복잡한 세상을 꿰뚫어 보는 통계물리학을 다룬 책 <세상물정의 물리학>을 펴내 대중과학작가로 이름을 알린 그가 이번엔 복잡한 인간관계의 원리를 찾아나서는 ‘인간관계의 물리학'을 4주마다 한번씩 연재한다.

누리 소통망을 들여다보면, 내 친구 중에는 정말 친구가 많은 사람이 있다. 또 내 친구들은 정말 바쁘게 사는 것처럼 보인다. 나도 꼭 한번 만나보고 싶은 사람들과 함께 소주잔을 기울이는 사진을 보니 참 부럽다. 여행은 또 왜들 그리 많이 가는지, 난 한번도 못 가본 여행지에서 찍은 사진을 떡하니 올리기도 한다. 나를 뺀 다른 친구들은 정말 분주하게, 의미 있고 행복한 삶을 사는 것 같다.

누리 소통망인 페이스북을 자주 이용한다. 나와 관심거리가 비슷한 사람이 많다. 뭐라도 나랑 겹치는 것이 많은 사람이 나와 친구가 될 가능성이 더 크니 당연한 일이다. 사정이 이렇다 보니, 내 친구들 여럿이 재밌어하는 소식은 나도 재밌다. 가만히 페이스북을 쳐다보고만 있어도 요즘 과학계에서 새로운 소식이 어떤 것이 있는지, 주변 과학자 중 누가 새 책을 냈는지, 내가 지지하는 정치인이 최근 어떤 활동을 하는지, 어렵지 않게 알 수 있는 시대다. 비슷한 연령대의, 비슷한 관심을 가진 사람들이 친구 중에 많아, 청소년을 열광케 할 아이돌 그룹 신곡 발표 얘기는 볼 수 없지만, 흥행에 처참하게 실패한 공상과학(SF)영화는 화제가 된다. 손바닥만한 스마트폰으로 누리 소통망을 잠깐 들여다보기만 해도, 세상 곳곳에서 벌어지고 있는, 내가 재밌어할 만한 따끈따끈한 새 소식을 들을 수 있다.

누리 소통망을 들여다보면, 내 친구 중에는 정말 친구가 많은 사람이 있다. 또 내 친구들은 정말 바쁘게 사는 것처럼 보인다. 나도 꼭 한번 만나보고 싶은 사람들과 함께 소주잔을 기울이는 사진을 보니 참 부럽다. 여행은 또 왜들 그리 많이 가는지, 난 한번도 못 가본 여행지에서 찍은 사진을 떡하니 올리기도 한다. 나를 뺀 다른 친구들은 정말 분주하게, 의미 있고 행복한 삶을 사는 것 같다.

편의점 삼각김밥으로 허겁지겁 점심을 때우며 들여다본 친구의 페북에는 지금 막 멋진 레스토랑에서 맛있는 식사를 하는 사진이 떡하니 올라 있다. 갑자기 삼각김밥을 먹는 내가 너무 초라해 보인다. 나뿐 아니라 많은 독자도 비슷한 경험을 할 때가 많을 거다. 오늘 이야기는 바로, 왜 내 친구는 친구가 많고, 또 내 친구는 왜 나보다 더 멋진 삶을 사는 것처럼 보이는지에 대한 이야기다. 글을 읽고 나서 많은 독자가 이런 느낌이 일종의 착시에 불과할 뿐이라는 것을 알게 되길 바란다. 어제 레스토랑 사진을 올린 친구는 오늘은 삼각김밥을 먹고 있다. 삼각김밥 사진을 올리지 않을 뿐이다. 어제 내가 삼각김밥 사진을 올리지 않은 것처럼.

알고 보면 간단한 ‘친구 관계의 역설’

세 명이 있다. A는 친구가 열 명, B는 친구가 한 명, 그리고 C도 마찬가지로 친구가 한 명이다. A의 친구 열 명에는 B와 C도 들어 있어서, B의 친구 딱 한 명이 바로 A고, C의 유일한 친구가 마찬가지로 바로 A다. 이 세 명에 대해서 친구 수를 나란히 적으면 10, 1, 1이다. 모두 더해 10+1+1=12이고, 3으로 나누면 4가 된다. A, B, C 세 명에 대해서 친구 수의 평균값은 4란 얘기다.(이 계산이 어려운 독자가 없기를 바란다. 잊어버렸을지도 모르지만 우리 모두 초등학생 때 이미 배운 거다.)

같은 상황에 대해서 이번에는 다른 계산을 해보자. 바로, 친구의 친구 수를 평균 내 보자는 얘기다. A에게 “네 친구는 친구가 몇 명이야?”라고 물어보자. A는 친구가 열 명이다. B와 C를 뺀 나머지 여덟 명의 친구 각각이 친구가 몇 명인지에 따라 답이 달라질 수는 있지만, 어쨌든 A의 답은 ‘1명’보다 작을 수는 절대로 없다. 마찬가지 질문 “네 친구는 친구가 몇 명이야?”를 B에게 물으면 B의 답은 ‘10명’, C에게 물으면 C의 답도 역시 ‘10명’이다.(기억하시는지. B는 친구가 딱 한명이고, 그 친구가 바로 친구가 10명인 A다. C도 마찬가지다.) 즉, “네 친구는 친구가 몇 명이야?”라고 묻고 각자가 답한 값을 나란히 적으면 1, 10, 10이 된다. 더하면 21, 3으로 나누면 평균값 7명. 자, 정리해보자. 친구의 친구 수의 평균값은 아무리 적어도 7명이다.

이쯤에서 뭔가 이상하다고 느낀 독자가 많을 거다. 친구 수의 평균은 4명인데, 어떻게 친구의 친구 수의 평균은 7명일 수 있을까. 왜 두 숫자가 많이 다를까. 이 두 숫자의 차이가 바로 ‘친구 관계의 역설’(Friendship paradox)에 해당한다. 각자에게 친구가 몇 명이냐고 물어보는 것과, 당신의 친구는 친구가 몇 명이냐고 물어보는 것이 다른 결과가 나온다는 것이 바로 친구 관계의 역설이다.

우리가 ‘역설’이라고 하는 것에는 사실 공통점이 있다. 언뜻 모순되어 보이지만 알고 나면 이상할 것이 없다는 것이 바로 공통점이다. 친구 관계의 역설도 마찬가지다. 왜 이런 역설이 생기는지는, 이런 역설이 생기지 않는 경우를 생각해보면 어렵지 않게 이해할 수 있다. 자, 서로서로 모두 친구인 다섯 명으로만 구성된 모임이 있다고 하자. 다섯 명 중 누구나 친구 수는 네 명이다.(다섯이 아니다. 이솝우화 <돼지들의 소풍>에서 자기를 빼고 숫자를 센 바로 그 엉뚱한 돼지처럼 세야 맞다. 자기는 자기의 친구가 아니다.) 누구나 예외 없이 친구가 네 명이니, 친구의 친구 수도 마찬가지로 네 명이다. 이 경우에는 친구 관계의 역설이 발생하지 않는다. 이처럼 각자의 친구 수가 큰 차이 없이 고만고만할 때는 친구 관계의 역설은 발생하지 않는다. 거꾸로 사람들 중 누군가가 친구가 아주 많을 때 역설이 발생한다. 이유도 어렵지 않다. 친구가 많은 마당발은 말 그대로 많은 사람과 친구다. 마당발의 그 많은 친구는 하나같이 “내 친구는 친구가 아주 많다”고 답하게 되기 때문이다.

딱 세 명만 있는 가상의 상황으로 친구 관계의 역설을 살펴봤다. 커다란 현실의 사회연결망에서는 어떨까. 공동연구자인 페터 홀메 교수가 제공한 약 3만명의 사람들로 이루어진 스웨덴의 한 누리소통망 데이터를 이용해서 우리 연구실의 이대경 연구원이 계산해봤다. 친구 수의 평균은 약 12명인데, 친구의 친구 수의 평균은 무려 230명이나 되었다.

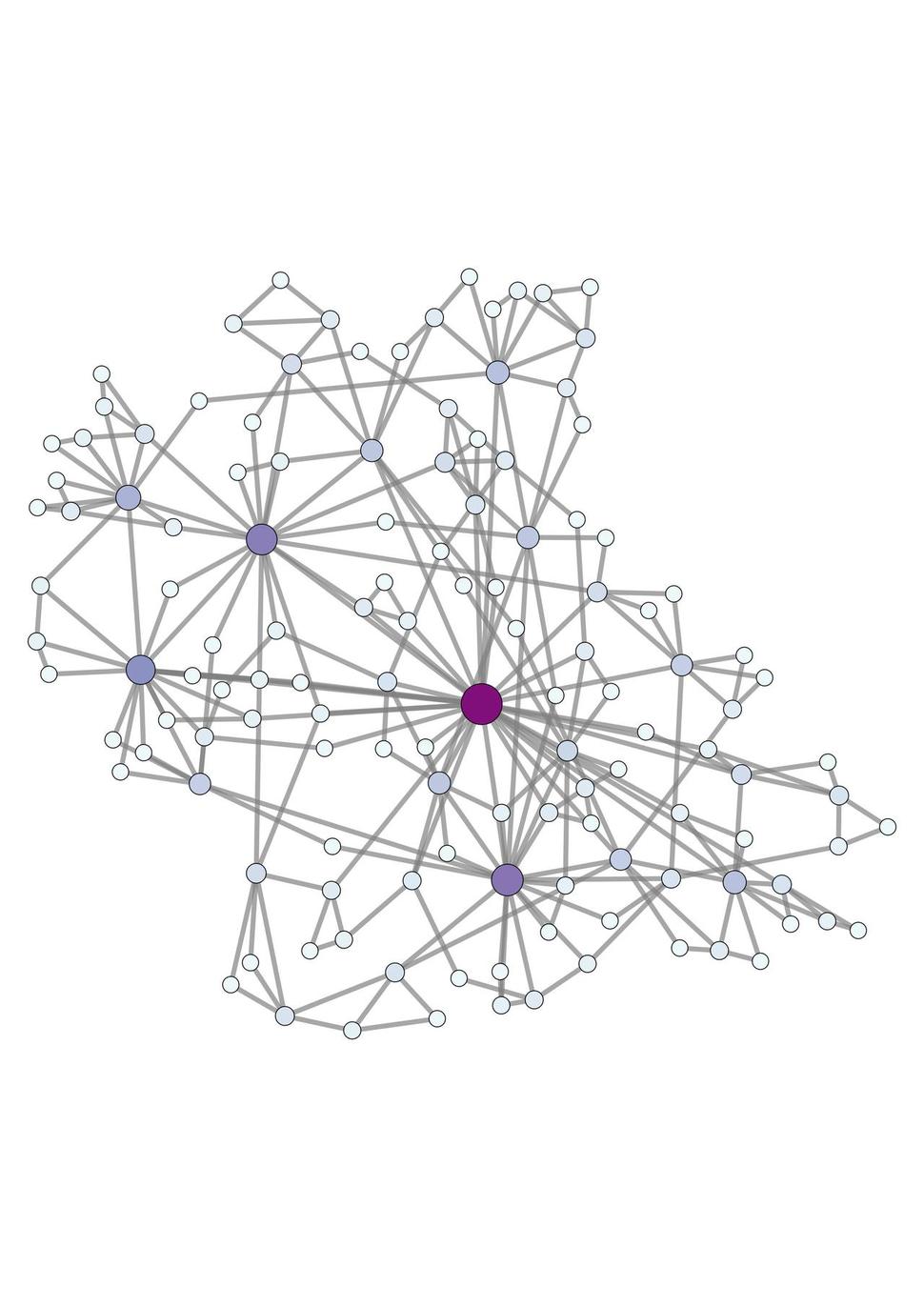
그림 1. 마당발이 있는 연결망. 김범준 제공

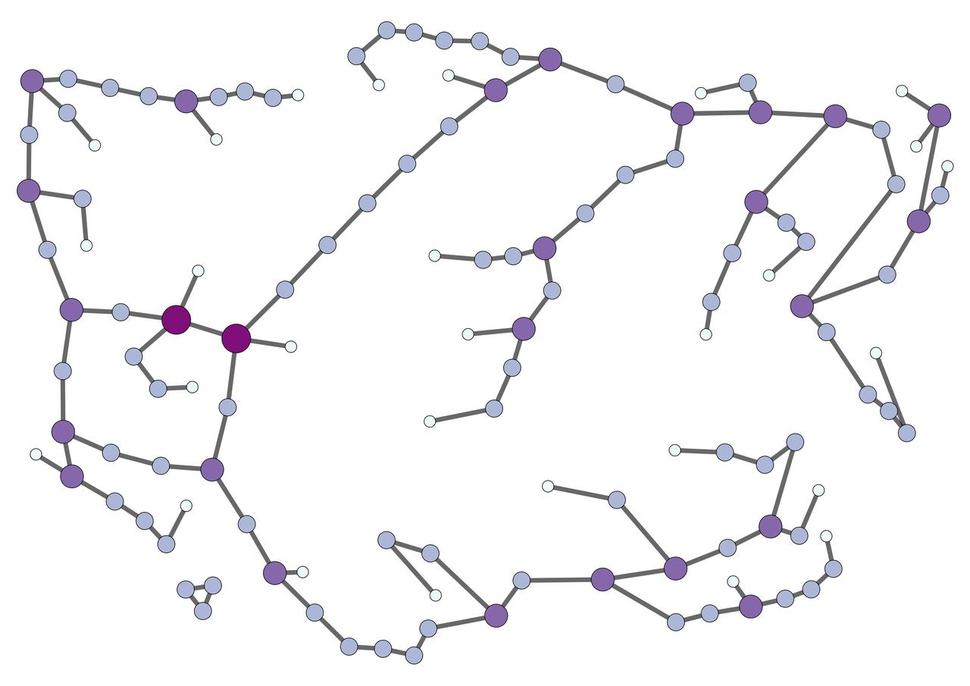
또 이 연구원은 컴퓨터 프로그램을 이용해서 마당발이 존재하는 연결망과 그렇지 않은 연결망을 각각의 모형을 이용해 만들어 같은 계산을 해봤다. 마당발이 있는 연결망의 경우([그림 1])에는 친구 수의 평균은 8명, 친구의 친구 수의 평균은 약 40명이었고, 마당발이 없는 고만고만한 연결망의 경우([그림 2])에는 친구 수 평균과 친구의 친구 수 평균이 둘 다 약 8명이라는 것을 알 수 있었다. 페이스북 친구가 몇 명 없는 독자가 독자의 친구는 친구가 정말 많다고 느끼는 것은 착시라는 얘기다. 독자가 친구보다 친구가 적다고 실망할 필요가 전혀 없다. 소수의 마당발을 뺀 누구나 마찬가지이기 때문이다. 페이스북의 연결망 구조에 마당발이 소수 있다는 것이 결론일 뿐이다.

그림 2. 마당발이 없는 연결망. 김범준 제공

왜 내 친구들은 항상 여행을 할까

친구 수 가지고 실망할 필요 전혀 없다는 이야기와 더불어, 왜 친구들은 나보다 맛있는 음식을 먹고, 나보다 여행을 많이 한다고 느끼는지도 살펴보자. 이 부분은 ‘선택 치우침’(selection bias)으로 쉽게 설명할 수 있다. 전혀 어려운 얘기가 아니다. 삼각김밥 먹는 사진을 올리는 사람은 없지만 1년에 딱 한번 가본 멋진 레스토랑 사진은 사람들이 올리기 때문이다. 친구 365명 각각이 1년 365일 중 딱 하루 가는 멋진 레스토랑 사진을 1년에 한번씩만 올려도, 독자는 매일매일 멋진 레스토랑에서 비싼 음식을 먹는 친구 누군가의 모습을 보게 될 뿐이다. 레스토랑 사진 속 그 친구도 독자와 마찬가지다. 364일은 독자가 오늘 먹는 평범한 점심을 먹는다.

‘선택 치우침’에 관련된 재밌는 일화가 있다. 2차 대전 당시 미군에서 전투에 투입되는 비행기의 어느 부분에 두꺼운 장갑을 둘러야 안전하게 보호할 수 있을지를 고민했다고 한다. 생환한 비행기의 총탄 자국을 살펴보니, 엔진 부분에는 거의 총탄 자국이 없고, 비행기 날개와 꼬리 부분에 총탄 자국이 많았다. 자, 그럼 엔진 부분은 장갑으로 보호할 필요가 없을까. 이 일화가 바로 명확한 ‘선택 치우침’ 효과를 보여준다. 엔진에 총격을 입은 비행기는 대부분 격추되어 살아 돌아오지 못하기 때문에 오히려 중요하지 않은 부분에 총격을 받은 비행기만 생환할 뿐이라는 얘기다. 합리적인 결론을 얻으려면 선택 치우침이 없는 자료를 모으는 것이 중요하다는 것을 알려주는 일화다.

페이스북에서 내 친구는 나보다 친구가 많다고 느끼는 것은 당연한 사실이다. 내가 정말로 친구가 적기 때문이 아니다. 페이스북에 마당발 친구가 있기 때문에 만들어지는 ‘친구 관계의 역설’ 때문이다. 페이스북에서 내 친구는 나보다 맛있는 식사를 하고, 멋진 장소를 여행하는 것처럼 보이는 것도 당연하다. 정말로 그 친구가 그런 멋진 삶을 사는 것이 아니다. 그런 예외적인 모습만 페이스북에 올리는 ‘선택 치우침’ 효과 때문이다. 어쩌면 스스로가 행복한지 아닌지를 다른 이와 비교해 판단하지 말자는 것이 더 중요한 결론일지도 모르겠다.

성균관대 물리학과 교수